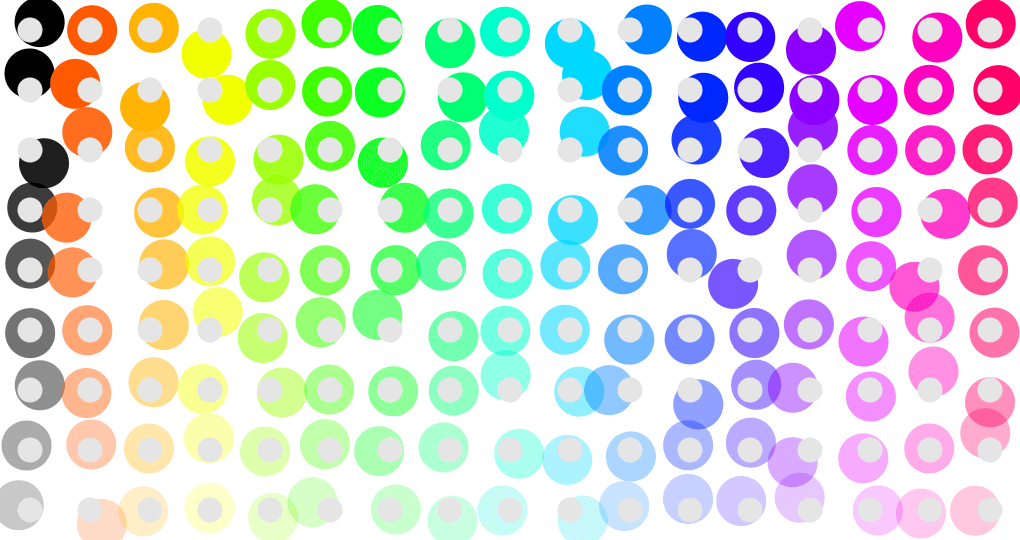第9弾では306個の円で180cm間隔のソーシャルディスタンスを表しましたが、さすがにウェブの画面だと小さすぎました。そもそも306個自体が多いので、円と円が重なっているとすれば153個の面積で済むので（理論のすり替えっぽい気もしますが）、17列x9行に2個ずつ円がある状態を考えてみました。出来上がりが以下。コードは画像の下。

※この記事は、7月までに三〇六輪100個作る企画の第10弾です。

//
// 初期値
//
// 輪の個数（9行x17個）
int maxY = 9;
int maxX = 17;
// 輪の直径、間隔
float diaBK = 50;　　// 大きな円
float diaFO = 25;   // 小さな円
float spX = 10;
float spY = 10;
// ウィンドウサイズ
int szx,szy;

//
// 描画ウィンドウサイズを決定する
//
void settings() {
  szx = int(diaBK+spX) * maxX;
  szy =int(diaBK+spY) * maxY;
  size(szx, szy);
}

//
// メイン処理
//
void setup() {
  float axisX, axisY, shiftX, shiftY, vars, varb, vara;
  colorMode(HSB,360,100,100,100);
  background(0,0,100,100);  
  translate(width/maxX/2, height/maxY/2); // 最初の円の中心を座標にする
  noStroke();
  randomSeed(0);                          // 乱数列を決定する
  
  // 大きな円を描く
  for (int itrY = 0; itrY < maxY; itrY++) {
    axisY = height/maxY * itrY;
    vara = 100/maxY * (maxY-itrY+1);
    for (int itrX = 0; itrX < maxX; itrX++) {
      axisX = width/maxX * itrX;
      shiftX = random(-1,1) * random(0,diaBK/2);
      shiftY = random(-1,1) * random(0,diaBK/2);
      if (itrX == 0) {
        vars = 0;
        varb = 0;
      } else {
        vars = 100;
        varb = 100;
      }
      fill(360/maxX*itrX,vars,varb,vara);
      ellipse(axisX+shiftX,axisY+shiftY,diaBK,diaBK);
    }
  }
  // 小さな円を描く
  for (int itrY = 0; itrY < maxY; itrY++) {
    axisY = height/maxY * itrY;
    vara = 100/maxY * (maxY-itrY+1);
    for (int itrX = 0; itrX < maxX; itrX++) {
      axisX = width/maxX * itrX;
      fill(0,0,90,70);    // 最後の引数は70です（投稿直後は100でしたが誤りです）
      ellipse(axisX,axisY,diaFO,diaFO);
    }
  }
  save ("306rin_010_" + str(int(diaBK))+ "_" + str(int(diaFO)) + ".png");
}

カラフルな大きな円は、第9弾のやり方と同じ。ただ前回HSBの0と360が同じ色（赤）になってしまったところを修正し、0なら黒にしました。円が重なるアイデアは「ジェエラティブデザイン　Processingで切り拓くデザインの新たな地平」という分厚い本にあったもの（P_2_1_2_02）から参考に。参考にした元では重なる2つの円の片方を固定してもう一方の中心をマウスで操作しながらインタラクティブにずらすというもの。当方のコードではずらす差分をインタラクティブではなくランダム値を与えて行うようにしました。

最初は、同じ中心に円を重ねてみて（写真1）、ずらす範囲はX座標Y座標共にゼロ〜半径分上下左右にOK（写真2）と考えました。ずらしてみると小さな円も透過した方が良さそうに思い、透過したものが最初の画像です。なお、上記コードでは投稿時はアルファを100と誤って書いていました。上記画像の通り透過しているので100ではなく70でした（コードは書き直しました）。

ちなみに、写真2と最初の写真（上の）の大きな円のズレ方が同じなのですが、randomSeedで乱数列を固定しているためです（これまた上述の本で知りました）。

このやり方だと重なりが2つだけでなく、3個、6個、9個などでも306個の円が作れるのですが、輪でないことに今気づきました（汗。